一些概念
- 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,
r[i] == r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的 - 时间复杂度:排序过程中对单个数据的访问总次数
- 空间复杂度:排序过程中需要辅助的存储空间
- 内部排序/外部排序:排序过程中数据元素是否完全在内存
结论最前
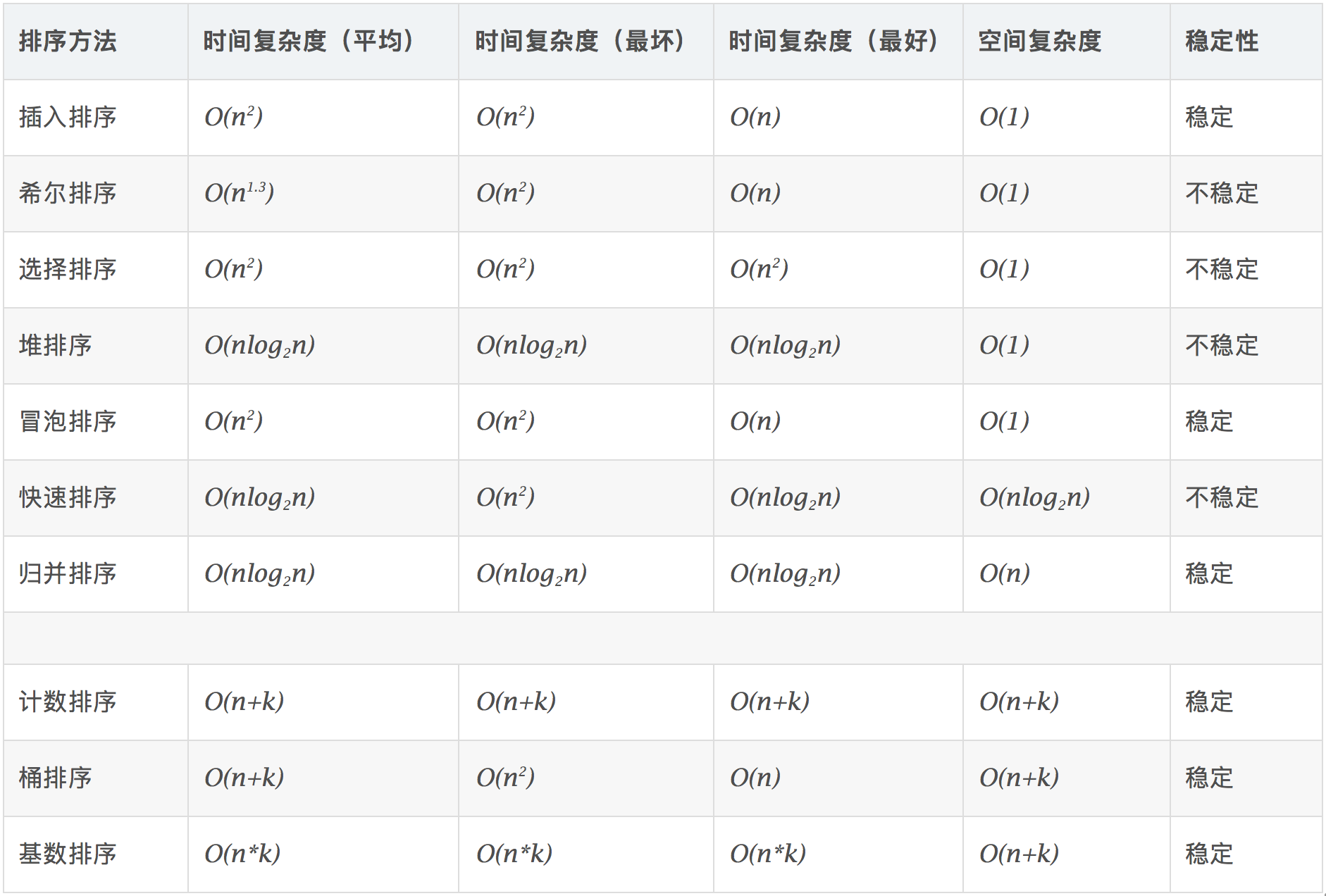
插入排序
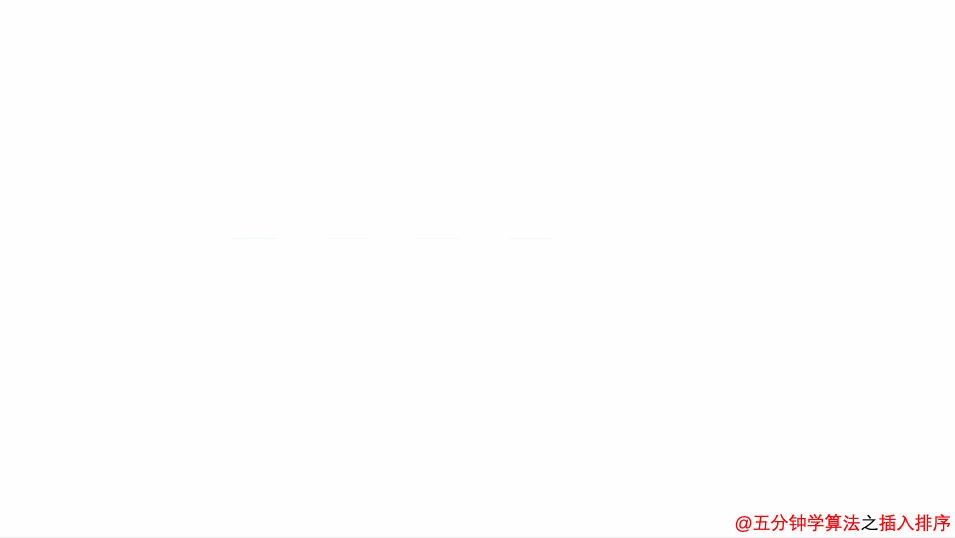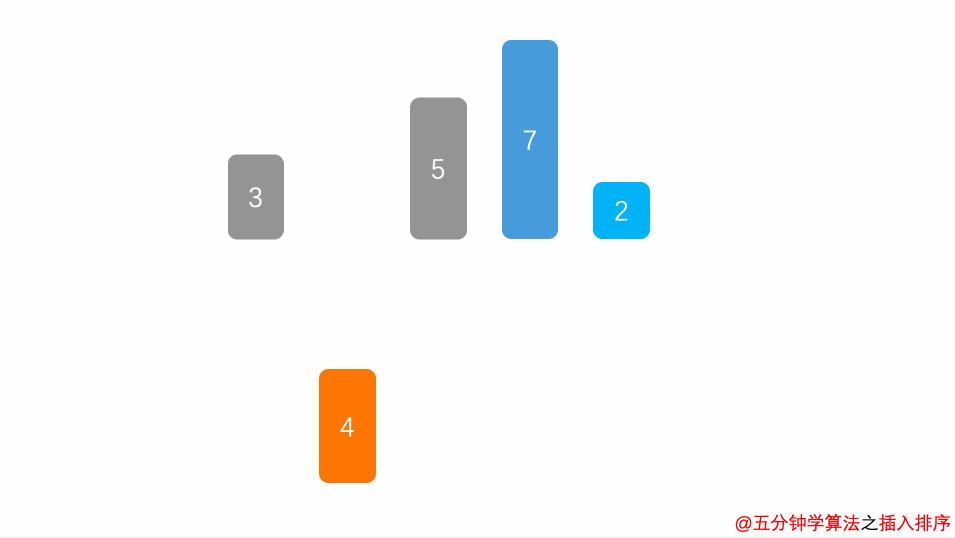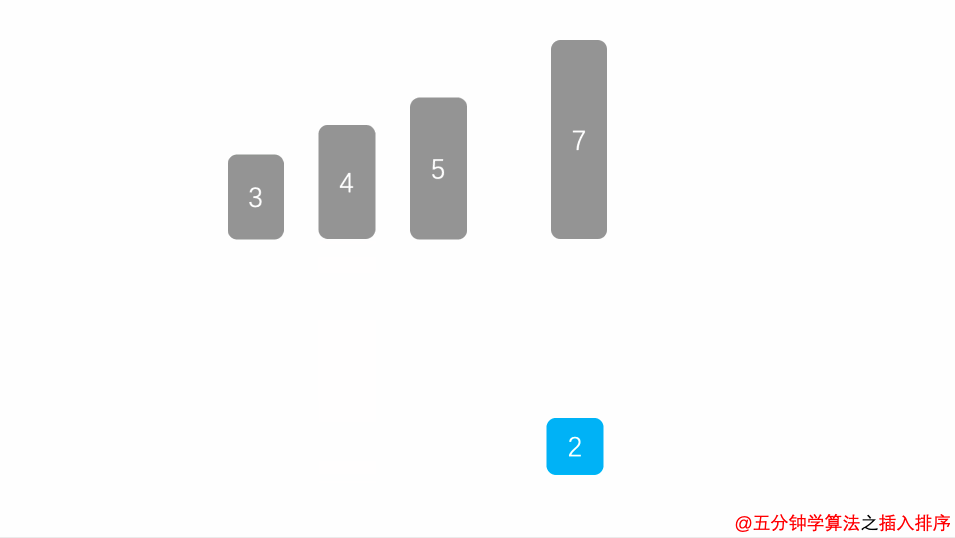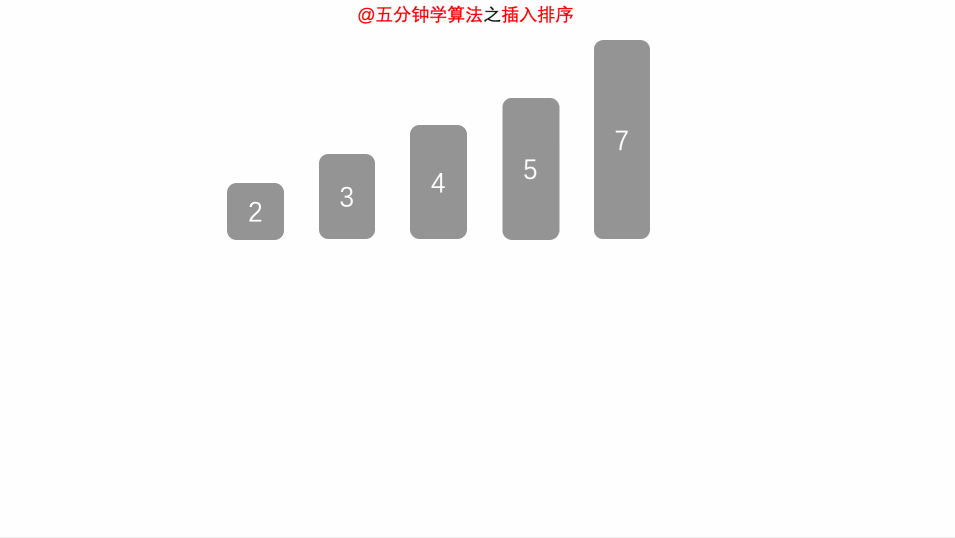
直接插入排序
算法:将第i个元素插入到前i-1个元素中适当的位置(选择插入位置时,因为前面元素已经有序,可以使用折半查找的方法)
可以考虑扑克牌的排序,抽取后面的牌插入到前面有序的牌中
性能分析:时间O(n^2^),空间O(1),稳定
图解
代码
1
2
3
4
5
6
7
8
9
10
11def insert_sort(nums):
for i in range(len(nums)):
j = i - 1
chosen_num = nums[i]
while j >= 0:
if nums[j] > chosen_num:
nums[j + 1] = nums[j]
else:
break
j -= 1
nums[j + 1] = chosen_num
希尔排序
算法
- 首先设定以
gap为距离对序列进行分组,对每个分组进行插入排序 - 缩小
gap(一般缩小为上次的1/2~1/3附近)重新排序,循环,直到gap缩小为1 gap为1的时候即为一次直接插入排序遍历
- 首先设定以
性能分析:时间O(n^1.3~2^),空间O(1),不稳定
图解

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17def shell_sort(nums) {
length = len(nums)
//区间
gap = 1
while gap < length:
gap = gap * 3 + 1 # 确保gap最终能够是1
while gap > 0:
for i in range(gap, length):
chosen_num = nums[i]
j = i - gap
//跨区间排序
while j >= 0 and arr[j] > tmp:
nums[j + gap] = nums[j]
j -= gap
nums[j + gap] = chosen_num
gap = gap / 3
选择排序
直接选择排序
算法:每次从待排序列中选择最小元素与待排序列首个元素交换后剔除首个元素,直到待排序列为空
性能分析:时间O(n^2^),空间O(1),不稳定
图解

代码
1
2
3
4
5
6
7def select_sort(nums):
for i in range(len(nums)):
min_index = i
for j in range(i + 1, len(nums)):
if nums[j] < nums[min_index]:
min_index = j
nums[i], nums[min_index] = nums[min_index], nums[i]
堆排序
堆:这里的堆指的是由完全二叉树实现的二叉堆
算法:首先将所给元素排成大顶堆,然后每次取根节点,然后进行删除调整大顶堆,由此得到顺序序列
性能分析:时间O(nlogn),空间O(1),不稳定
图解

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45// golang
// 堆插入,生成大根堆结构
func HeapInsert(nums []int) {
for i := 1; i < len(nums); i++ {
childIndex := i
parentIndex := (childIndex - 1) >> 1
for childIndex > 0 && nums[parentIndex] < nums[childIndex] { // O(logN)
nums[parentIndex], nums[childIndex] = nums[childIndex], nums[parentIndex]
childIndex = parentIndex
parentIndex = (childIndex - 1) >> 1
}
}
}
// 堆调整,将大根冒泡
func HeapAdjust(nums []int, to int) {
if to == 0 {
return
}
cur := 0
for {
leftChildI := cur<<1 + 1
if leftChildI > to { // nums[to] is the max num
break
}
rightChildI := leftChildI + 1
tobeChildI := leftChildI
if rightChildI < to && nums[rightChildI] > nums[leftChildI] {
tobeChildI = rightChildI
}
if nums[cur] < nums[tobeChildI] {
nums[cur], nums[tobeChildI] = nums[tobeChildI], nums[cur]
cur = tobeChildI
continue
}
break
}
}
// 堆排序
func HeapSort(nums []int) {
HeapInsert(nums)
for i := len(nums) - 1; i > 0; i-- {
nums[0], nums[i] = nums[i], nums[0]
HeapAdjust(nums, i-1)
}
}
交换排序
冒泡排序
算法:通过从后往前的交换,将较小元素交换到待排序列最前端,每次“冒泡”可确定一个最小元素的位置
性能分析:时间O(n^2^),空间O(1),稳定
图解

代码
1
2
3
4
5
6
7
8def bubble_sort(nums):
n = len(nums)
for i in range(n):
j = n - 1
while j > i:
if nums[j] < nums[j - 1]:
nums[j], nums[j - 1] = nums[j - 1], nums[j]
j -= 1
快速排序
算法
- 核心思想为分治法,从序列中选出一个基准值,其他依次和基准做比较,比基准大的放右边,小的放左边
- 然后分别对左右两边再次使用快速排序
- 单边扫描
- 我们随意抽取一个数作为基准值,同时设定一个标记 mark 代表左边序列最右侧的下标位置,当然初始为 0
- 接下来遍历数组,如果元素大于基准值,无操作,继续遍历,如果元素小于基准值,则把 mark + 1 ,再将 mark 所在位置的元素和遍历到的元素交换位置
- mark 这个位置存储的是比基准值小的数据的最后一个,当遍历结束后,将基准值与 mark 所在元素交换位置即可
性能分析:时间O(nlogn),空间O(logn),不稳定
图解

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37// 划分,将数组划分为大于基准值,等于基准值,小于基准值三个部分
func partition(nums []int, from, to int) (midl, midr int) {
left := from - 1
right := to
cur := from
for cur < right {
if nums[cur] < nums[to] {
nums[cur], nums[left+1] = nums[left+1], nums[cur]
left += 1
cur += 1
} else if nums[cur] > nums[to] {
nums[cur], nums[right-1] = nums[right-1], nums[cur]
right -= 1
} else {
cur += 1
}
}
nums[to], nums[right] = nums[right], nums[to]
right += 1
return left + 1, right - 1
}
// 随机基准值快排
func QuickSort(nums []int) {
rand.Seed(time.Now().UnixNano())
pivot := rand.Int63n(int64(len(nums)))
nums[pivot], nums[len(nums)-1] = nums[len(nums)-1], nums[pivot]
quickSort(nums, 0, len(nums)-1)
}
// 快排递归结构
func quickSort(nums []int, from, to int) {
if from >= to {
return
}
midLeft, midRight := partition(nums, from, to)
quickSort(nums, from, midLeft-1)
quickSort(nums, midRight+1, to)
}
归并排序
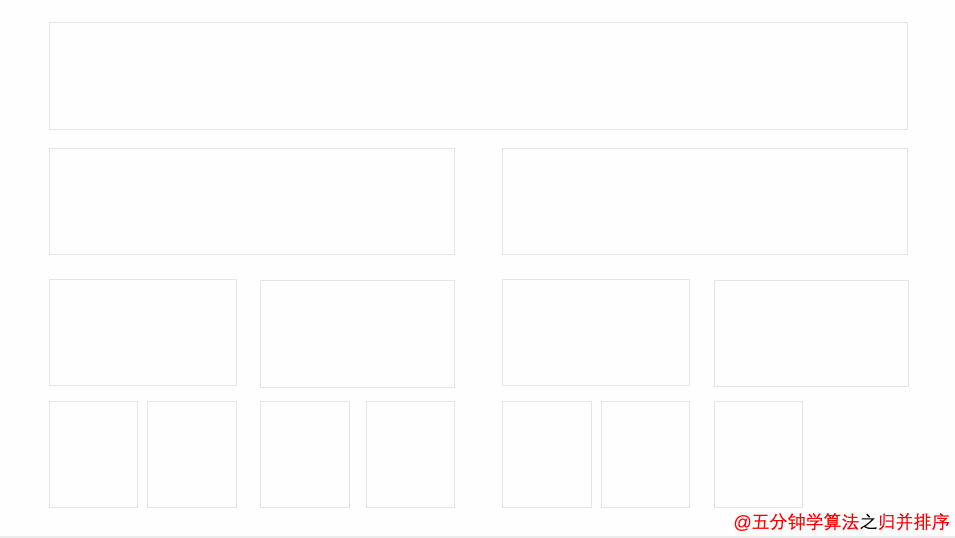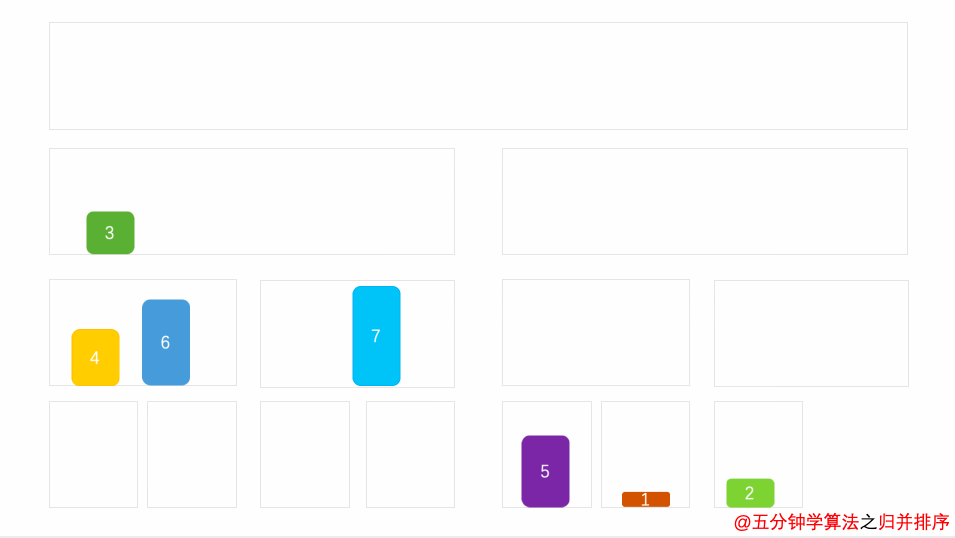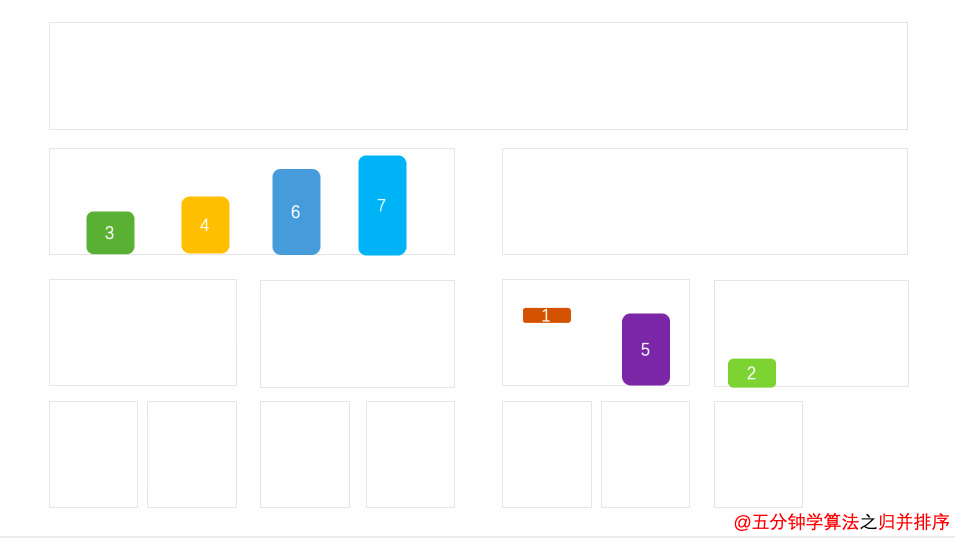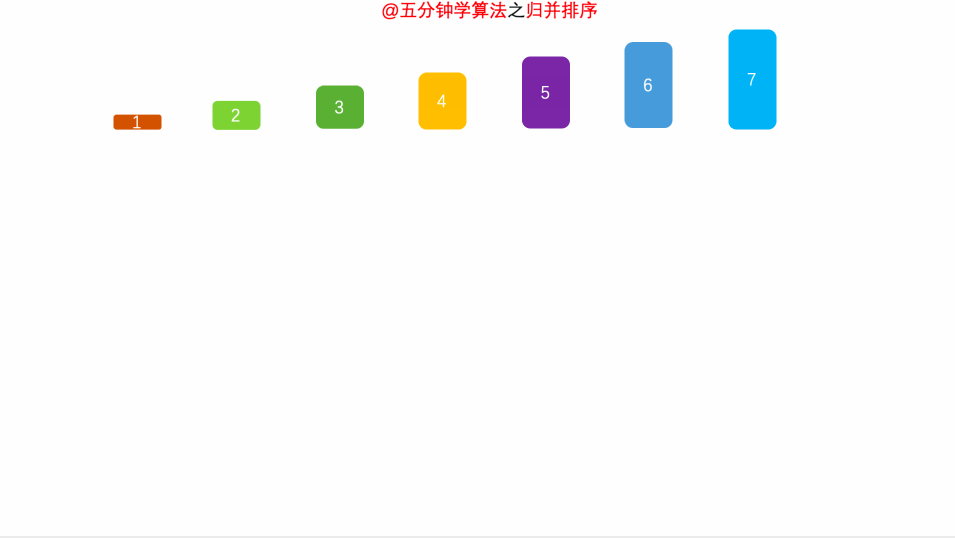
算法:将待排序列分为两部分,对左右两部分分别进行归并排序,然后将两个有序序列合并为一个有序序列
性能分析:时间O(nlogn),空间O(n),稳定
图解
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35// golang
func merge(nums1, nums2 []int) []int {
i, j := 0, 0
res := make([]int, 0, len(nums1)+len(nums2))
for i < len(nums1) && j < len(nums2) {
if nums1[i] < nums2[j] {
res = append(res, nums1[i])
i++
} else {
res = append(res, nums2[j])
j++
}
}
if i < len(nums1) {
res = append(res, nums1[i:]...)
}
if j < len(nums2) {
res = append(res, nums2[j:]...)
}
return res
}
func MergeSort(nums []int) []int {
if len(nums) <= 1 {
return nums
}
mid := len(nums) / 2
leftPart := MergeSort(nums[:mid])
rightPart := MergeSort(nums[mid:])
return merge(leftPart, rightPart)
}
分类排序
计数排序
算法:对于待排序列首先选择其最大和最小值,创建一个计数区,计算在最大和最小值之间所有数字出现的次数,最后以计数桶顺序还原有序序列
性能分析:时间O(n),空间O(max-min),不稳定
图解
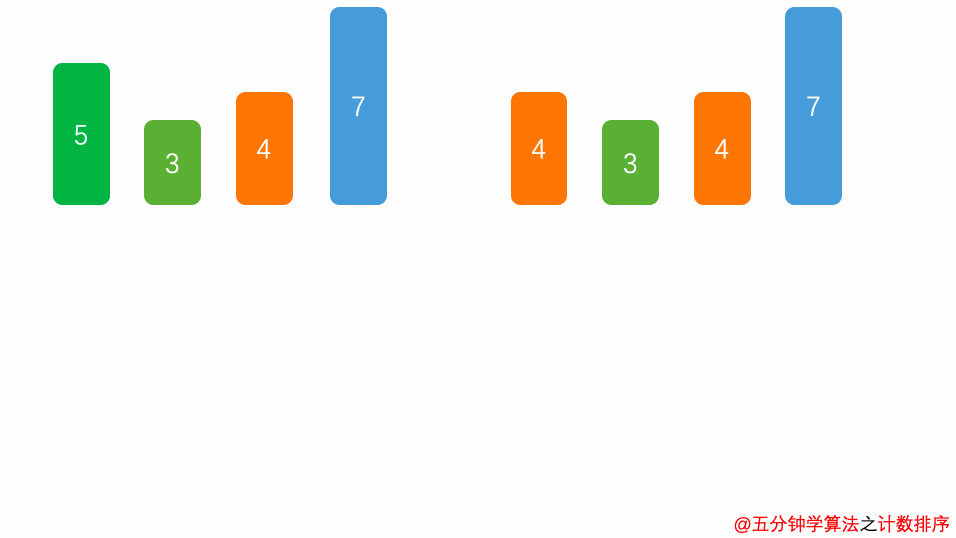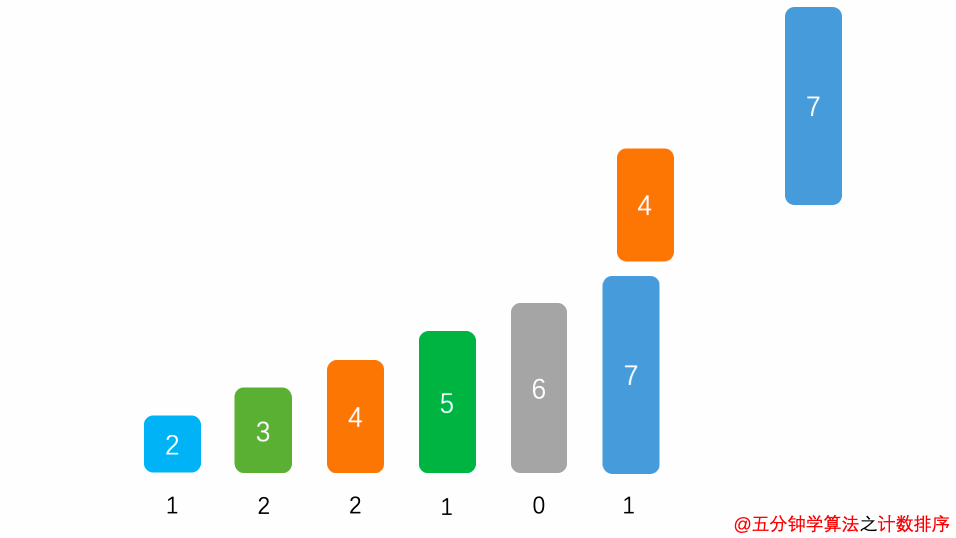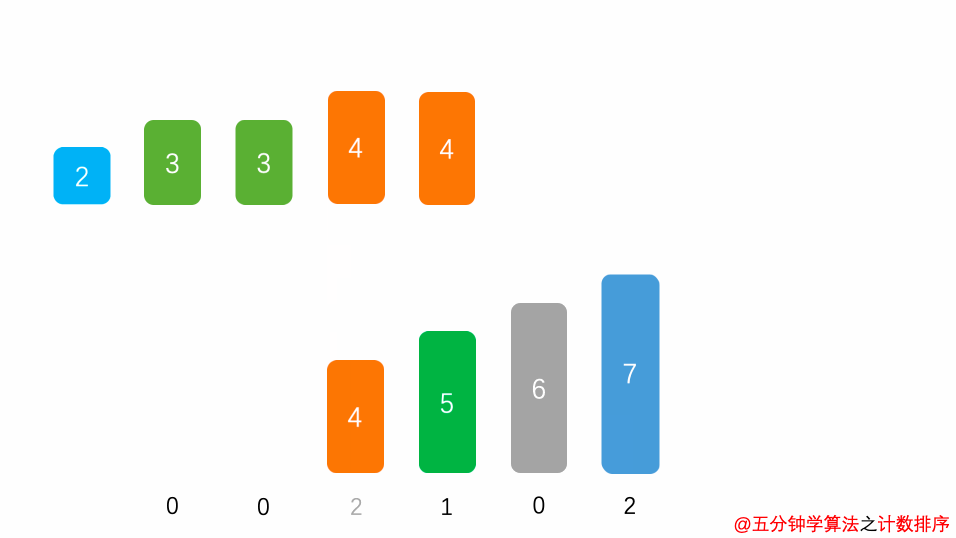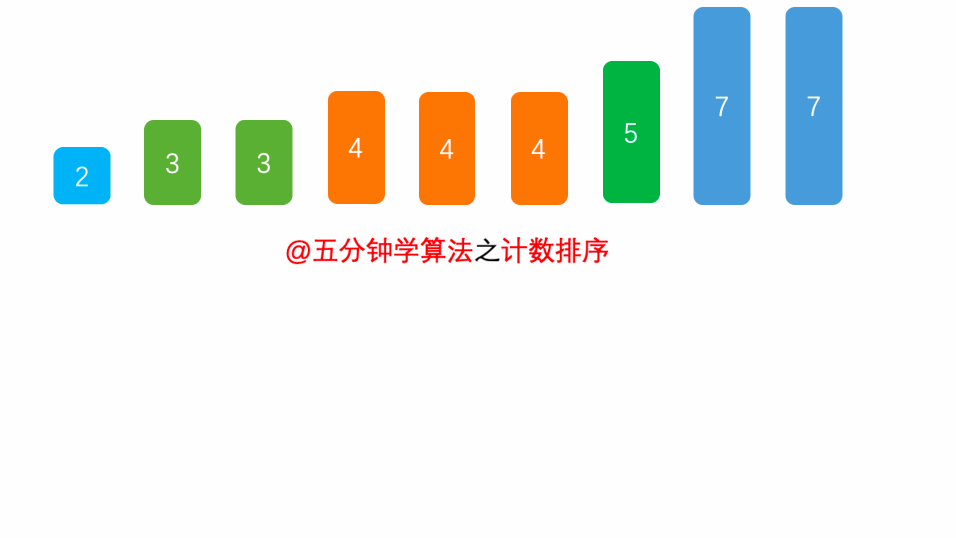
代码
1
# todo
桶排序
算法
- 将要排的数据分到多个有序的桶里
- 每个桶里的数据再单独排序,再把每个桶的数据依次取出,即可完成排序
性能分析:时间根据桶的粒度会有不同变化,空间:桶的数目
图解

基数排序
算法
- 按照位数,分别对每位进行比较,放入对应的桶内,然后将桶内元素以先进先出的方式按桶序取出
- 如此经过d次(d为最大位数)排序后即可得到顺序
- 本算法需要待排序列有基数,并且基数可排序
性能分析:时间:O(d*n),空间O(d*n),稳定
图解

代码
1
# todo